Have a good time!
MinhNguyen 
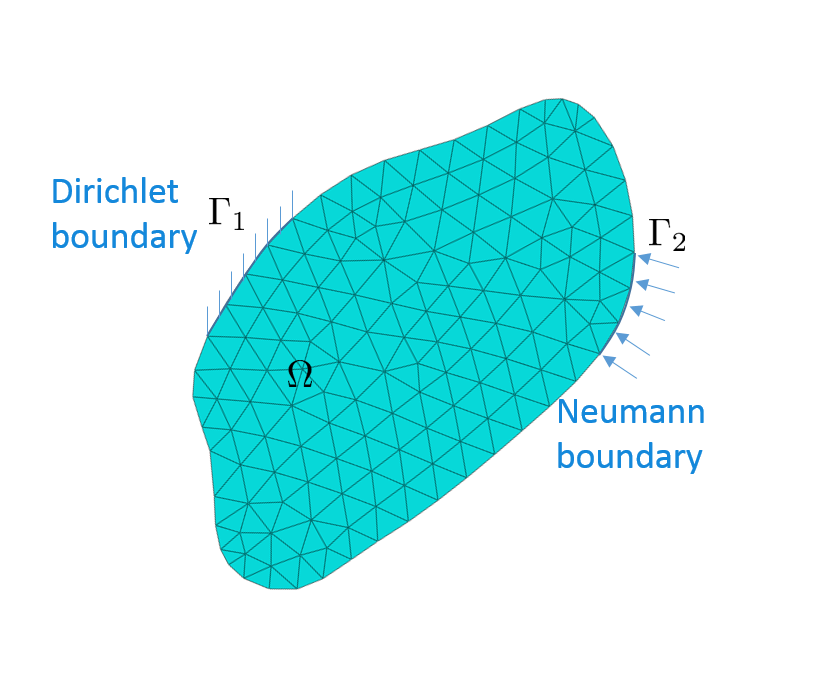
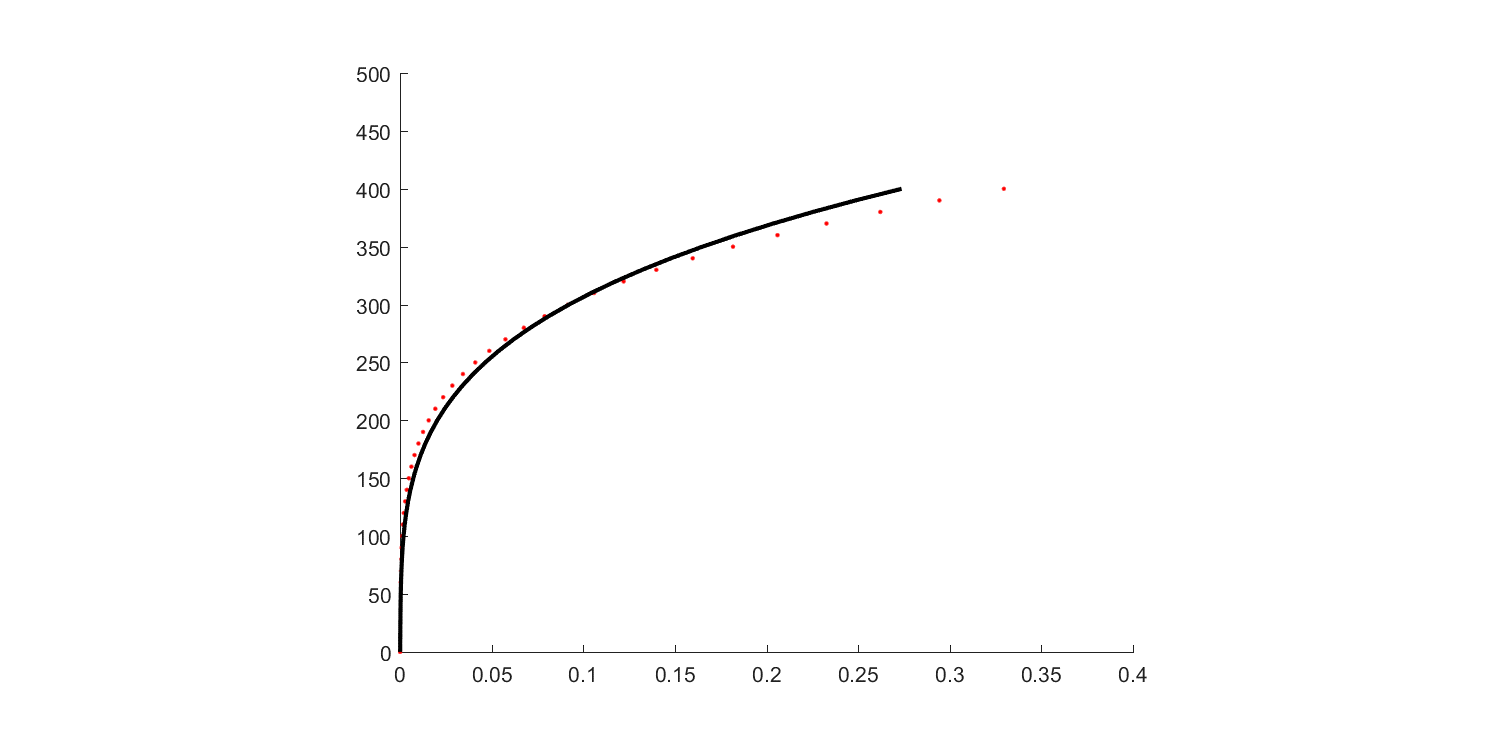
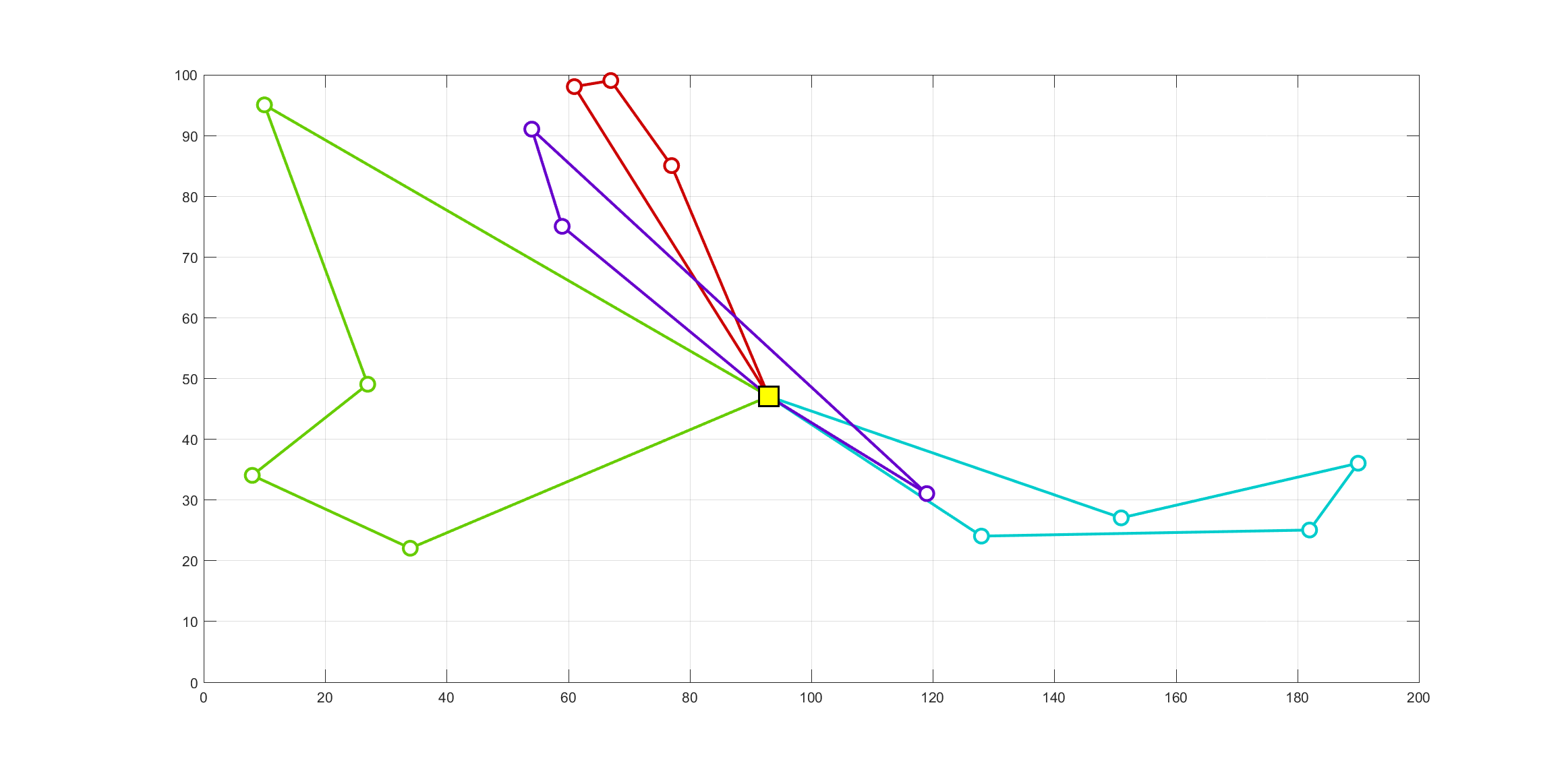
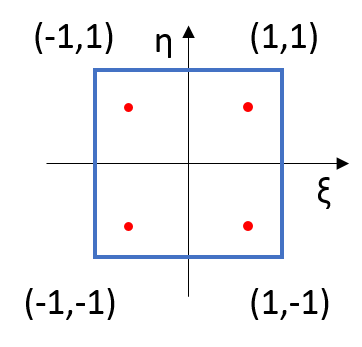
Strong formulation (or Strong form): the partial differential equation that governs the problem. For example: the equilibrium equation in solid mechanics, the Fourier’s equation for transport of thermal energy, the Fick’s law for mass transport, etc. Below is the equilibrium equation in solid mechanics, which satisfies at every point of the problem domain. $\nabla \cdot … Read more
Parameter identification is usually encountered in engineering. Some types of problems are listed below. Curve fitting. This is a simple problem when we only have to find the relation between two sets of data: $x$ and $y$. The most common example would be “linear regression”, such that we assume a linear relation: $y = ax … Read more
The Routing vehicle problem (RVP) can be considered as a generalization of the Traveling salesperson problem (TSP). It short, the objective is to find the optimal routes for multiple vehicles to visit a set of locations. The objective is to minimize the total cost of multiple trucks (the number of trucks is known beforehand and … Read more
The Gaussian quadrature for a square domain ([-1, 1] x [-1, 1]) can be conducted by a similar manner to 1D integration (see 1D Gaussian quadrature) $\int \limits_{-1}^{1} \int \limits_{-1}^{1} g(\xi,\eta) d\xi\eta \approx \sum_{i=1}^{n} \sum_{j=1}^{n} g(\xi_i, \eta_j) w_i w_j$, where $\xi$ and $\eta$ denotes the coordinate in horizontal and vertical direction, respectively. Theoretically, the number … Read more